http://10.107.0.68/~jgche/ 单电子近似 1 第三(四)章、能带理论——前言 • 是固体物理的核心其基础是三大近似 * 绝热近似、单电子近似、周期性势场近似 • 绝热近似(附录)原子核比电子重得多，跟不 上电子运动；考虑电子运动时，原子核固定 • 周期性势场近似晶体结构的周期性(第2章) • 单电子近似？ * 在金属自由电子气中，实际上已用了单电子近似 独立电子近似电子与电子之间没有相互作用 * 现在，需要考虑电子与电子之间的相互作用 * 如何考虑多电子问题？  还需要作些近似处理单电子近似 http://10.107.0.68/~jgche/ 单电子近似 2 本讲目的：强调观念转变带来的… • 多电子转化为单电子问题的两种处理方法 * Hartree-Fock近似  过程可以清楚地看出多电子问题的困难在哪里？ 单电子近似解决了什么，又留下什么问题？ * 密度泛函理论  观念带来的变化，但仍未解决问题，关键何在？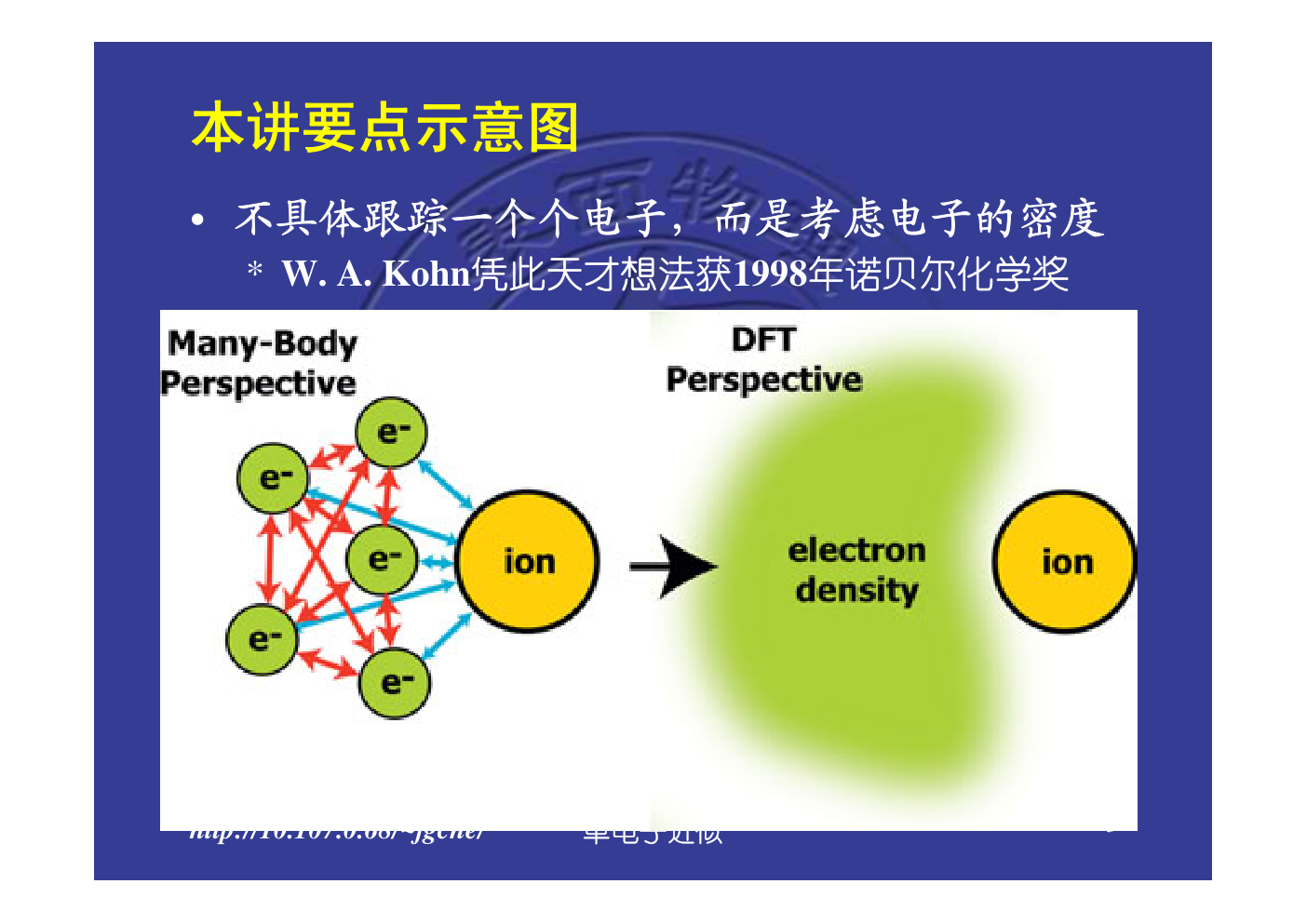  注意：密度泛函理论不是单电子近似，是其基础 • 观念转变  不是一个个电子，而是电子密度作为核心物理量 来研究多电子体系 http://10.107.0.68/~jgche/ 单电子近似 3 本讲要点示意图 • 不具体跟踪一个个电子，而是考虑电子的密度 * W. A. Kohn凭此天才想法获1998年诺贝尔化学奖 http://10.107.0.68/~jgche/ 单电子近似 4 http://10.107.0.68/~jgche/ 单电子近似 5 http://10.107.0.68/~jgche/ 单电子近似 6 第13讲、单电子近似(专题二) 1. Hartree-Fock方程(Hartree, 1958, Fock, 1960) * 平均场近似单电子方程 * Koopman定理 2. 密度泛函理论(1964，W. Kohn) * Kohn-Sham方程单电子方程 * 交换关联能 附录、绝热近似多电子Schoedinger方程 http://10.107.0.68/~jgche/ 单电子近似 7 1、Hartree-Fock方程 • 如何描写电子之间的相互作用？ * 多电子Schroedinger方程 * 写成单电子算符和双电子算符 • 如果没有交叉项，问题就很简单 • 可用单电子波函数的乘积组成多电子波函数， 称为Hartree波函数               i i i i ii i i i i i ii i i r E r H H r r V m i                                 ' ' ' ' 2 2 ˆ ˆ 1 2 1 2 r r          i i i i r E r H     ˆ           N N i r r r r     ... 2 2 1 1  http://10.107.0.68/~jgche/ 单电子近似 8 • 代入后，令E=ΣEi, 分离变量后即可得单电子 方程 • 形式上这就是单电子方程。可是，如果有交叉 项就不可能这样分离变量，但依然可以认为 Hartree波函数仍是一个好的近似，或说多电 子波函数可用它展开，代入多多电子方程 • 用变分法，可得Hartree方程 * 已用原子单位，即令     i i i i r E r H    ˆ ' ' ' ' ˆ 2 1 ˆ i i ii ii i i i i i i H H E                       r r r r r r r r i i i j i j E d V                     ' ' ' 2 2 1 2 ,1 ,1 2    m e  http://10.107.0.68/~jgche/ 单电子近似 9 • 但，电子需满足Pauli不相容原理；电子是费米 子，交换反对称！ Hartree波函数没有考虑 • 这就是Fock对此修正：交换行列式任何两行， 行列式变号满足交换反对称。这个行列式称 为Slater行列式 • 用这个行列式计算能量的期待值，用变分法， 最终可得到Hartree-Fock方程                       N N N N N N i r r r r r r r r r N r           ,..., , ... ,..., , ,..., , ! 1 2 1 2 2 2 2 1 1 1 2 1 1                        r r r r r r r r r r r r r r i i j j i j i j i j i E d d V                    ' ' ' ' ' ' ' * 2 2 Fock的修正 http://10.107.0.68/~jgche/ 单电子近似 10 思考：什么是关联？看方程形式 • 这就是关联！ * 因为第i个电子的方程包含另一个电子 的指标， j，而且以求和的方式与所有 其他电子有关，也即依赖于其他所有 电子的解，这N个电子的解互相关联， 需要解N个联立方程组                       r r r r r r r r r r r r r r i i j j i j i j i j i E d d V                    ' ' ' ' ' ' ' * 2 2 http://10.107.0.68/~jgche/ 单电子近似 11 自洽求解 • 积分号中含有解，所以一般用自洽求解的方 式，就是先假定一个解，得到积分，再解薛定 谔方程，得到更好的解 * 不断重复这个过程直至这个解在一预先规定的精度 内不再变化——达到自洽自洽解                       r r r r r r r r r r r r r r i i j j i j i j i j i E d d V                    ' ' ' ' ' ' ' * 2 2 http://10.107.0.68/~jgche/ 单电子近似 12 如要去掉求和号中j≠i的限制 • 这只需要在第3项增减一项j=i即可， * 多出的一项并入第2项，也成对所有电子求和                                                 r r r r r r r r r r r r r r r r r r r r r r r r r r r r r r i i i j j i j i i i i i i i j j i j d d d d d                ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' * * * * *                   r r r r r r r r r r r r r r i j j i j j i j i E d d V                  ' ' ' ' ' ' ' * 2 2                       r r r r r r r r r r r r r r i i j j i j i j i j i E d d V                    ' ' ' ' ' ' ' * 2 2 http://10.107.0.68/~jgche/ 单电子近似 13 进一步处理 • 前面第二项是其他电子对i电子的库仑相互作用 • 第三项是交换项，如分子分母乘以同样的项 * 这样就可以在形式上写成关于第i电子的方程 * 但这只是形式上的                            j i i i j i i j j j i j d d r r r r r r r r r r r r r r r r           * * * * ' ' ' ' ' ' ' '                     r r r r r r r r r r r r r r r r i i j i i i j j i j j E d d V                            * * * 2 2 ' ' ' ' ' ' ' http://10.107.0.68/~jgche/ 单电子近似 14 平均场近似 • Slater建议再对i求平均，即看作单个电子在其 他所有电子的平均势场下的运动，即 • 这就是平均场或称有效场近似——单电子方程                  ' , ' ' * ' ' * * ' ' ' ' ' i j i i i i i j j i d r r r r r r r r r r                                          ' , ' ' * ' ' * * ' 2 eff eff 2 2 ' ' ' ' ' ' ' ) ( ) ( ) ( ) ( 2 i j i i i i j j i j j i i i d d V V E V m r r r r r r r r r r r r r r r r r r           http://10.107.0.68/~jgche/ 单电子近似 15 单电子方程对所有电子都相同 • 现在这个方程还有电子关联吗？ • 试在上式中变换电子指标，i，方程不变！ 对所有电子，都是同一个方程！不再依赖于其他所 有电子的解！仅剩一个独立的方程 1. 单个电子满足的方程；其他所有电子(包括该电子 本身，因求和遍及所有电子) 对该电子作用被平均 2. 对所有电子都相同，所以其解也可用于其他电子                 ) ( ) ( ' ' ' ' ' ' ' 2 ' , ' ' * ' ' * * ' 2 2 2 r r r r r r r r r r r r r r r r i i i i j i i i i j j i j j E d d V m                            http://10.107.0.68/~jgche/ 单电子近似 16 Koopmans定理 • H-F方程中的Ei在前面是作为拉格朗日乘子出 现的，它有什么物理意义？ • 试将第i个电子从系统中移走，因为1029数量级 的电子，所以从中移走一个电子可以假定不改 变其他单电子i’≠i波函数；求能量期待值的变 化 • 前一项就是将波函数行列式的第i行第i列去 掉，只有i’和i’=i的项被保留 ) ( ) ( ) ( 2 eff 2 2 r r r i i i E V m              http://10.107.0.68/~jgche/ 单电子近似 17 • 所以整理后，可以得到 • 式中的Ei具有单电子能量的意义。- Ei相当于移 走一个电子所需要的能量。也即将一个电子从i 态移到k态所需能量为Ek - Ei * 这就是Koopmans定理 http://10.107.0.68/~jgche/ 单电子近似 18 评论：Hartree-Fock方程 • 在作平均场近似前 1. 方程既包括了电子之间的交换作用Slater行列式 中交换行或列，都只差一符号 2. 方程也包含了电子之间的关联作用每个电子的解 是依赖于其他电子的解的，需要解联立方程组 • 但在固体中，这样的方程组将涉及到1029/m3 量级的方程，无法求解 * Slater建议对所有电子对该电子的作用进行平均 * 作平均时也包含了该单电子本身的作用 * 平均后，没有了电子之间的关联！ 多电子问题就以这样的方式演变为单电子方程 http://10.107.0.68/~jgche/ 单电子近似 19 H-F方程解决了什么问题？ 多电子问题！ 多电子问题经过平均场近似的处理后，变 成了单电子问题！ http://10.107.0.68/~jgche/ 单电子近似 20 单电子是指整个体系只有单个电子？ 并非整个体系只有单个电子，而是指所 有的电子都满足同样的方程——单电子 方程！ 单电子方程被用来处理多电子问题。只不 过所有电子都满足同样的方程，因此，只 需解一个方程就等于得到所有电子的解了 http://10.107.0.68/~jgche/ 单电子近似 21 从多电子方程到H-F方程，整个过程 非常繁复，困难来自哪里？ 困难在于一个个电子考虑问题！ http://10.107.0.68/~jgche/ 单电子近似 22 http://10.107.0.68/~jgche/ 单电子近似 23 2、密度泛函理论 • 密度泛函理论的基本思想：把电荷密度当作一 个基本物理量。由两个定理组成 * 定理1：多电子系统基态的物理性质是由电子密度 决定的 * 定理2：电子数不变时，能量泛函对电子密度的变 分可以得到系统基态的能量 * 这里能量泛函形式为 * 分别为动能、库仑能、交换关联能泛函 ] [ ' )' ( ) ( ' 2 1 ] [ ] [      xc G E d d T E      r r r r r r http://10.107.0.68/~jgche/ 单电子近似 24 定理一证明 • 定理1：多电子系统基态的物理性质是由电子 密度决定的 • 定理一的核心：电子密度函数是决定系统基态 物理性质的基本变量。 * 即除一附加常数外，v(r)是电子密度函数的唯一泛 函 * 电子密度函数定义为，Ψ(r)是产生、湮灭算符             r r r  http://10.107.0.68/~jgche/ 单电子近似 25         r r r r v v d E V V H H H E                ' ' ' ' ' ' '          r r r r v v d E E     ' '          r r r r ' ' ' ' ' ' ' ' v v d E V V H H H E                         r r r r ' ' v v d E E      • 用反证法。假定另外存在一v’(r)，也具有同样 的电子密度函数，我们需证明这是不可能的 * 即对v’ (r)，有 * 而对v (r)，有 * 两式相减得，E+E’