两个平行四边形倾斜的角度可能不同,周长不一定相等,但面积相同。那么,如何在几何画板中验证这一结果呢?让我们来看看使用几何画板来验证同一底部等高平行四边形面积的相等方法。
具体操作:
选择新的几何画板文件“线段直尺工具”,按住Shift键,画一条水平直线。在直线外任取一点,选择点和直线,执行“构造”——“平行线”。
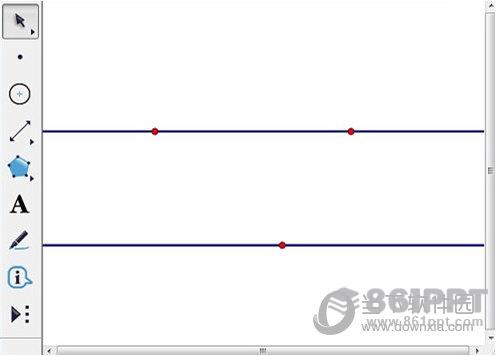
在直线外任取两点A、B,选择两个点A、B和直线,“构造”——“垂线”,垂直于平行线的两点C、D,依次选择中点A、B、C、D,“构造”——“线段”,得到矩形ABCD。依次选择中点A、B、C、D,“构造”——“四边形内部”。
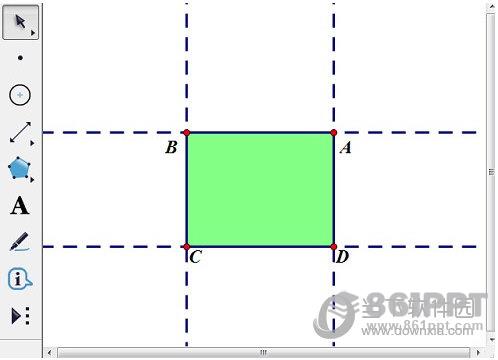
在点A所在的直线上任命一点F,选择点C、F,“构造”——“线段”,获取线段CF,选择线段CF和点D,“构造”——“平行线”,交线在一点E,依次选择中点C、D、E、F,“构造”——“四边形内部”。

选择矩形ABCD内部,“度量”——“面积”ABCD面积=19.21平方厘米;同样,选择CDEF内部,“度量”——“面积”CDEF面积=19.21平方厘米。平行四边形CDEF面积与矩形ABCD面积相同。
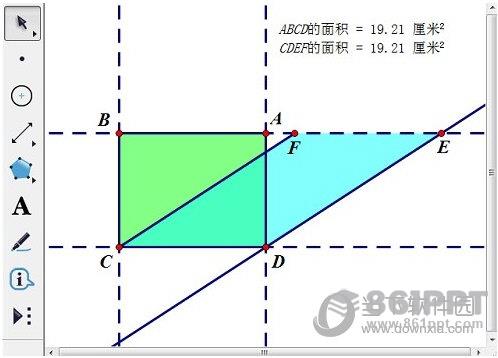
以上教程介绍了用几何画板验证同底等高平行四边形面积的方法。操作并不复杂。你可以通过练习几次来掌握方法。